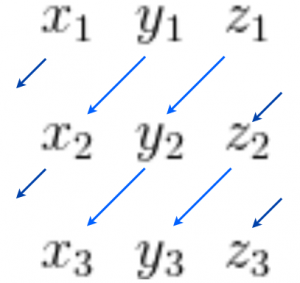正方行列に対して決まるスカラー値

行列Aの行列式を\det Aや|A|と表記する

具体例

A=\left( \begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right)の行列式は、a_{11} a_{22}-a_{12} a_{21}

A=\left( \begin{array}{lll}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right)の行列式は、\begin{array}{l}{a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}} {-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}}\end{array}

覚え方

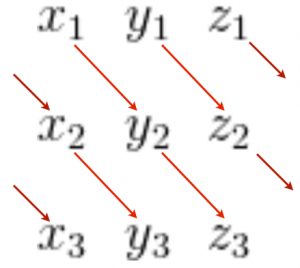
左上から右下に向けてかけて足す、右上から左下に向けてかけて引く

以下の図がわかりやすい

こういうやり方のことをサラスの方法と呼ぶ

性質

単位行列の行列式は1: det I = 1

i列とj列を交換すると行列式は-1倍される

なんかあったなこれ、忘れた

一つの列以外固定して一つの列の関数と見たときに線形性が成立する。

行列式の転置不変性

行列Aの転置行列^tAをとっても行列式は等しい

\det A=\det {}^tA

参考