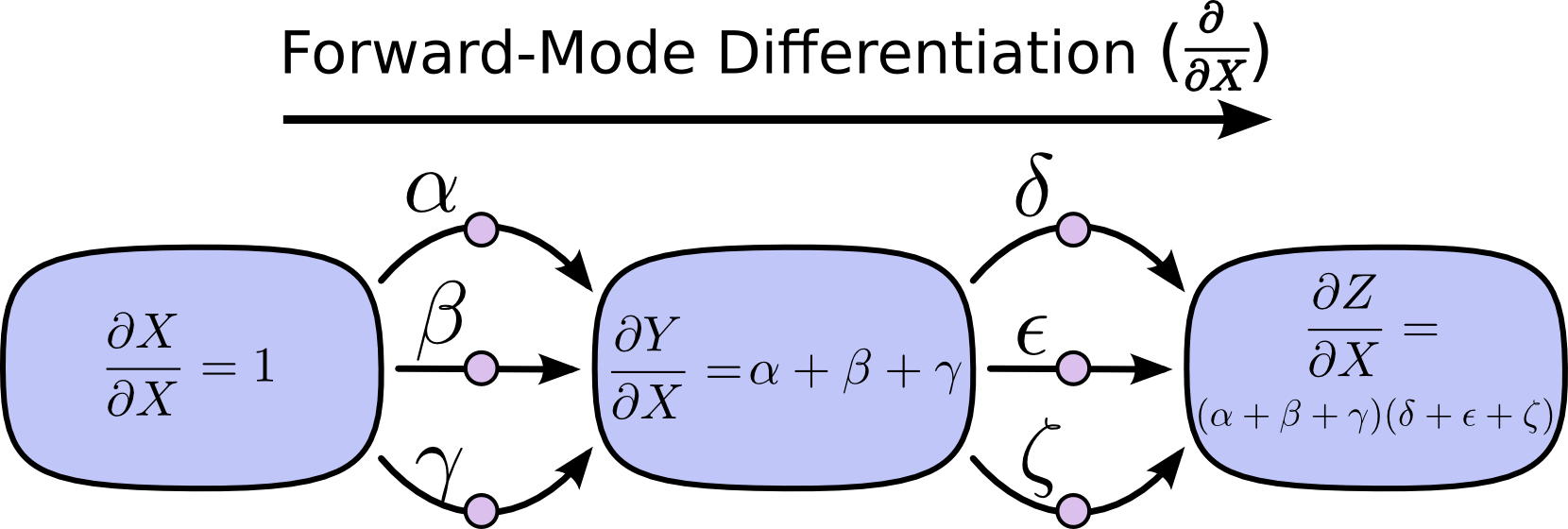自動微分
Automatic differentiation
> プログラムで定義された関数を解析し、偏導関数の値を計算するプログラムを導出する技術 ref
数学的に正確
フォワードモードの自動微分
計算グラフの入力から出力向かって計算する
ある入力が各ノードにどのように作用するのかを追跡する
全ての各ノードに\frac{\partial}{\partial 入力}を適用する
出力の次元が入力の次元より大きいときは効率がいい
悪い方の例
100万の入力、1つの出力のとき
微分係数を得るためにグラフを100万回行き来する必要がある
各ノードで\frac{\partial}{\partial X}が求まる
リバースモードの自動微分
グラフの出力から入力へ向かって計算する
各ノードがある出力にどう作用するのかを追跡する
全ての各ノードに\frac{\partial 出力}{\partial}を適用する
入力の次元が出力の次元より大きいときは効率がいい
ニューラルネットワークでは、入力の次元が大きいことが多いので、よくこちらが使われる
各ノードで\frac{\partial Z}{\partial}が求まる
用途
機械学習フレームワーク
自動車工学
気候モデリング
etc.
Haskellで実装
参考
===============================================================
この辺の記事と統合する
めっちゃ詳しい
しらべる
これについて
Haskellで実装
38行
pytorch
参考
rust