高校数学Ⅰ【二次関数】「きみは誰?」
ロイロ 鍵本 優紀
高校数学の二次関数の授業案です。
既習事項やわかっていることの整理⇨自分のアイデアの発散⇨シンキングツールで分析・収束という流れを繰り返しています。
「答えが1つになるからシンキングツールが使いにくい」としばしばいわれてしまう数学ですが、たとえ答えは1つであっても、その思考過程は自由に発散できるのではないかと思い作成しました。
授業案
シンキングツール使用のポイント
生徒の今考えていることをシンキングツールに書き出して整理するという基本にこだわりました
題材についてポイント
二次関数の単元全体をとりあつあかっています
誰しもがとりあつかうところ、「ここってシンキングツールどうやってつかうの?」って思うところに挑戦しました。
二次関数というよりも、「関数とは何か」を理解してほしいという意図もあります
概要
全体の流れ
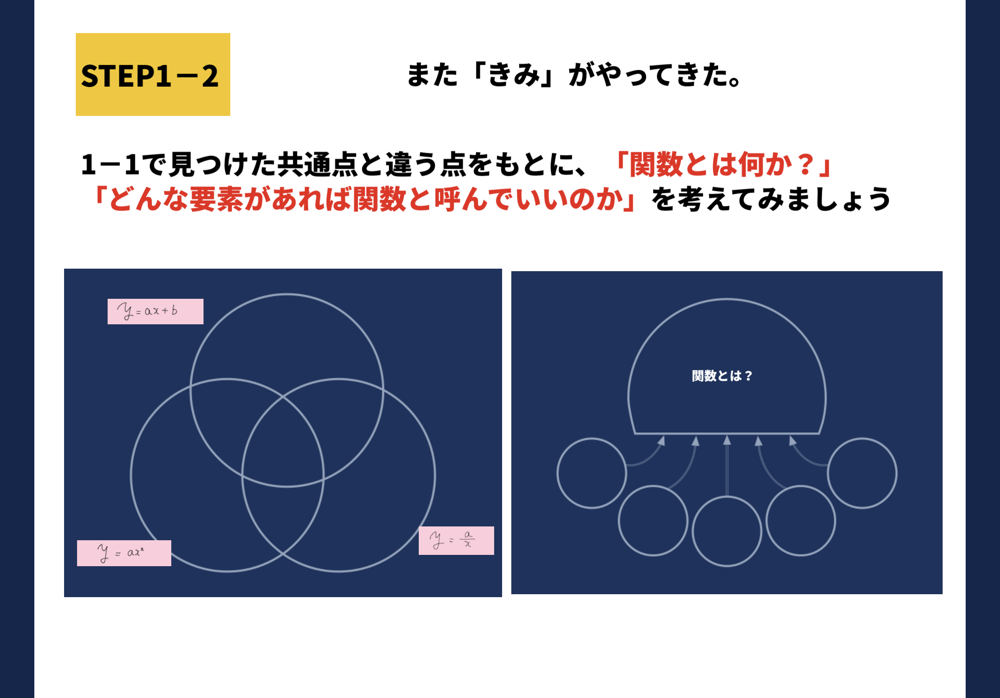
STEP1 関数とは何か?
これまでとりあつかってきた、一次関数・原点固定の二次関数・反比例を題材に、それぞれの共通点と相違点をあげてもらいます。そこから「関数とは何か?」を考えてもらいます。
「関数とは何か?」をまずは子供達なりにまとめてもらったあとで、関数の定義を再度確認します
さらに、これまで関数について習った用語などについても各自でまず整理をします
STEP2 今回の二次関数のグラフをかこう
中学校で習った原点固定の二次関数と今回新規でならう二次関数を比べて、グラフの書き方を考えます。
まずは、どのように動かせばかさなりそうか、「言葉」で説明してもらいます
そのあと、式でそれを表現する方法を考えます
このあと、平方完成した式のグラフを書く問題演習を行います
STEP3 一般式から平方完成させよう
一般式から平方完成をする方法を考えます。
まずは、平方完成をした式から展開をさせて、そこから逆に辿ることで平方完成をする方法を考えます。
各班で考えた平方完成方法を共有して、平方完成の方法をまとめます。
各班で方法をまとめたあとで、正規の平方完成の手順を伝えて、問題演習をおこないます
STEP4 二次方程式と二次関数
二次方程式と二次関数の関連を考えてみます。
STEP5 二次関数と解の個数
いろいろな二次関数のグラフをかいて、解の個数をしらべてみます。
あえて解の個数と表現せずに、「困ったやつ」はどれかという振り方で考えます
各班で、グラフの形と解の個数の関係を予想して、説明してもらいます
各班でグラフの形と解の個数を説明したあとで、判別式などとの関連を説明して、問題演習をおこないます
STEP6 二次関数と放物線
二次関数が身の回りに「あらわれてしまう」例として、「放物線」をとりあげます。
なぜ放物線が二次関数の形になってしまうのか考えてもらいます