三角関数
三平方の定理
a^2 + b^2 = c^2(cは斜辺)
特殊な直角三角形の比
45^\circ:45^\circ:90^\circ = 1:1:\sqrt{2}
30^\circ:60^\circ:90^\circ = 1:\sqrt{3}:2
三角関数
なぜ使うか?:図形計算の簡略化
直角三角形による定義は0 < \theta < \frac{2}{\pi}まで。単位円による定義だと任意の実数まで拡張可能。
早見表
| 関数 | 日本語 | 覚え方 |
| sine | 正弦 | SOH: Sine Opposite over Hypotenuse |
| cosine | 余弦 | CAH: Cosine Ajacent over Hypotenuse |
| tangent | 正接 | TOA: Tangent Opposite over Ajacent |
| cosecant | 余割 | sinの逆数 |
| secant | 正割 | cosの逆数 |
| cotangent | 余接 | tanの逆数 |
hypotenuse(斜辺), opposite(対辺), adjacent(隣辺)
\sin(\theta) = \frac{\mathrm{opposite}}{\mathrm{hypotenuse}}
\cos(\theta) = \frac{\mathrm{ajacent}}{\mathrm{hypotenuse}}
\tan(\theta) = \frac{\mathrm{opposite}}{\mathrm{ajacent}}
csc, sec, cotはそれぞれsin, cos, tanの逆数
asine acos, atanとの違い: arcは逆関数
\csc(\theta) = \frac{\mathrm{hypotenuse}}{\mathrm{opposite}}
\sec(\theta) = \frac{\mathrm{hypotenuse}}{\mathrm{ajacent}}
\cot(\theta) = \frac{\mathrm{ajacent}}{\mathrm{opposite}}
Alfredで計算する場合: sin, cos, tan関数はdegreeをradianに変換して渡す 1\degree = \frac{\pi}{180}\ \mathrm{rad}
=sin(θ * pi/180) =cos(θ * pi/180) =tan(θ * pi/180) 三角関数の還元公式
余角
\sin(\theta) = \cos(90\degree-\theta)
\cos(\theta) = \sin(90\degree-\theta)
\frac{1}{\tan(\theta)} = \tan(90\degree-\theta)
補角
\sin(\theta) = \sin(180\degree - \theta)
-\cos(\theta) = \cos(180\degree - \theta)
-\tan(\theta) = \tan(180\degree - \theta)
特殊な直角三角形から
有名角の形に直せば電卓なしで計算できる
30\degree = \frac{\pi}{6}
45\degree = \frac{\pi}{4}
60\degree = \frac{\pi}{3}
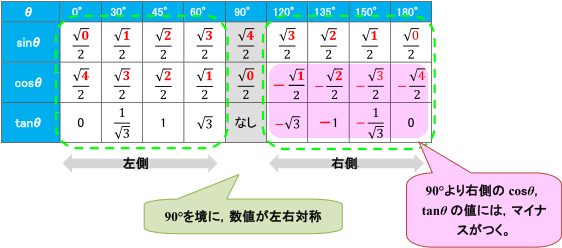
有名角の三角比の覚え方
加法定理
\sin(a+b) = \sin(a)\cos(b) + \sin(b)\cos(a)
\sin(a-b) = \sin(a)\cos(b) - \sin(b)\cos(a)
\cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b)
\cos(a-b) = \cos(a)\cos(b) + \sin(a)\sin(b)
\tan(a+b) = \frac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)}
\tan(a+b) = \frac{\tan(a)-\tan(b)}{1+\tan(a)\tan(b)}
倍角公式
\cos2\theta = \cos^2\theta - \sin^2\theta = 2\cos^2\theta - 1 = 1 - 2\sin^2\theta
\sin2\theta = 2\sin\theta\cos\theta
\tan2\theta = \frac{2\tan\theta}{1-\tan^2\theta}
逆三角関数
なぜ使うか?:直角三角形の2辺から角度θを求めることができる
\sin^{-1} (\frac{\mathrm{opposite}}{\mathrm{hypotenuse}}) = \theta
\cos^{-1}(\frac{\mathrm{ajacent}}{\mathrm{hypotenuse}}) = \theta
\tan^{-1}(\frac{\mathrm{opposite}}{\mathrm{ajacent}}) = \theta
三角関数は複数の入力が同じ出力を持つため、本来は可逆関数ではない
e.g. \sin(0) = \sin(\pi) = 0
逆関数を定義するためには定義域を制限する必要がある
Alfredで計算する場合、asin, acos, atan関数はradianで返ってくるので必要ならdegreeに変換 1rad = \frac{180}{\pi}\degree
=asin(opposite/hypotenuse) * 180/pi =acos(ajacent/hypotenuse)* 180/pi =atan(opposite/ajacent) * 180/pi 正弦定理・余弦定理