下の「ロマネスコ」というカリフラワーのように、全体と一部分が同じような形をしているものを「フラクタル構造」といいます。「フラクタル」という言葉は数学者のBenoît B. Mandelbrot氏が提唱したものです。海岸線の構造のようにフラクタル的な性質をもつものは世の中に広く見られるので、数学的/科学的に興味深いうえに、簡単に美しいCGを生成できるといった様々な工学的応用もあります。

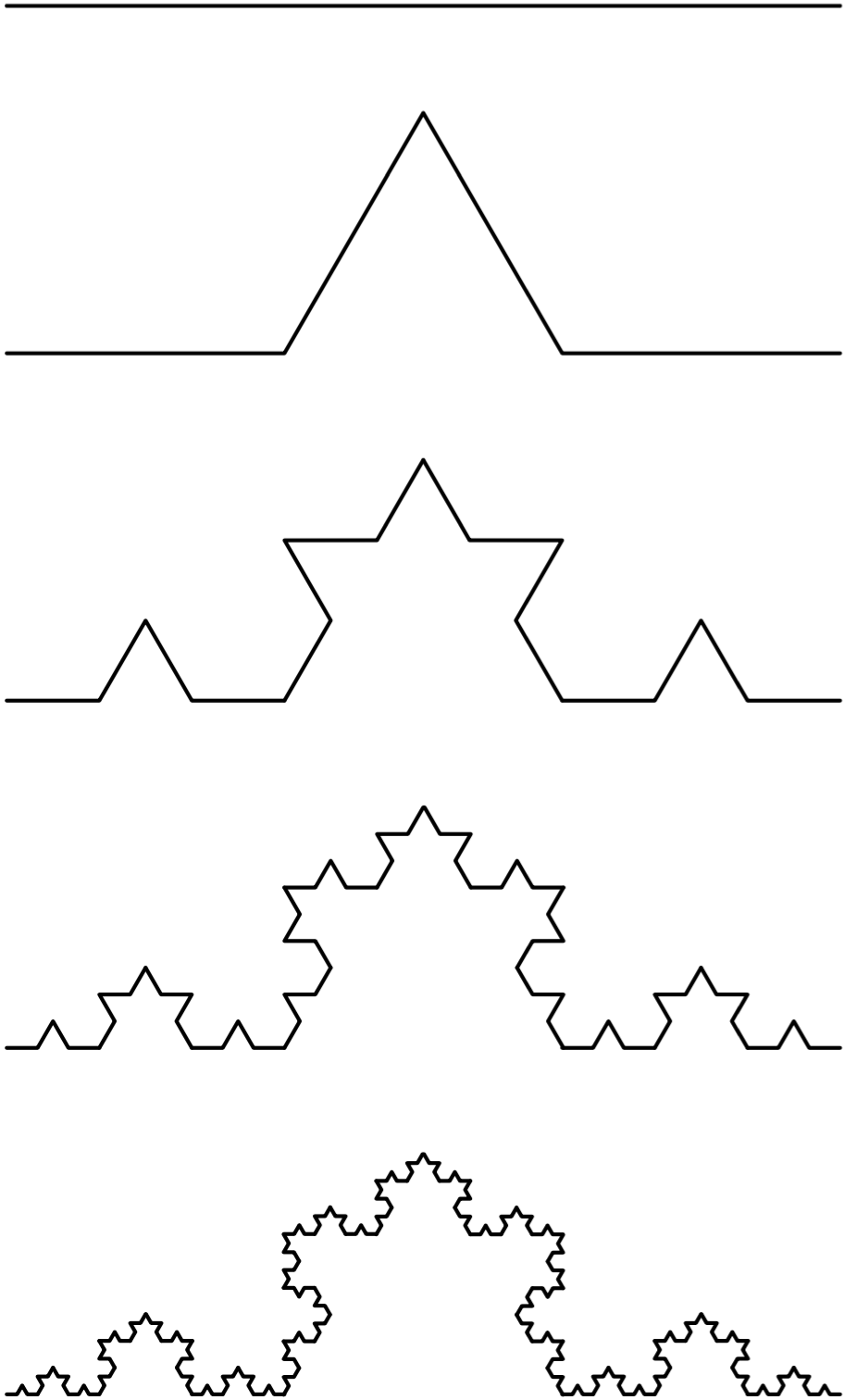
　比較的単純なフラクタル構造として、左図のように直線を3分割して折り曲げることを無限に繰り返してできる「コッホ曲線」というものが知られています。 縮尺を大きくするたびに折り曲げを行なうことにすると、 縮尺を3倍にすると長さは4倍、縮尺を9倍にすると長さは16倍...という具合に縮尺と長さは変化しますが、長さと縮尺の対数をとると、その比は常にlog(4)/log(3)=1.2618という一定の値になり、この値はフラクタル次元と呼ばれます。

　このような関係をもつふたつの数値を両対数グラフ上にプロットするとグラフが直線になりますが、プロットしたグラフが直線になるような関係があるとき、これらは冪乗則(べきじょうそく, Power Low)(「冪乗」とは「2の3乗」のように「XをY回掛ける」ような計算)フラクタル構造をもつ図形のパラメタは冪乗則に従います。

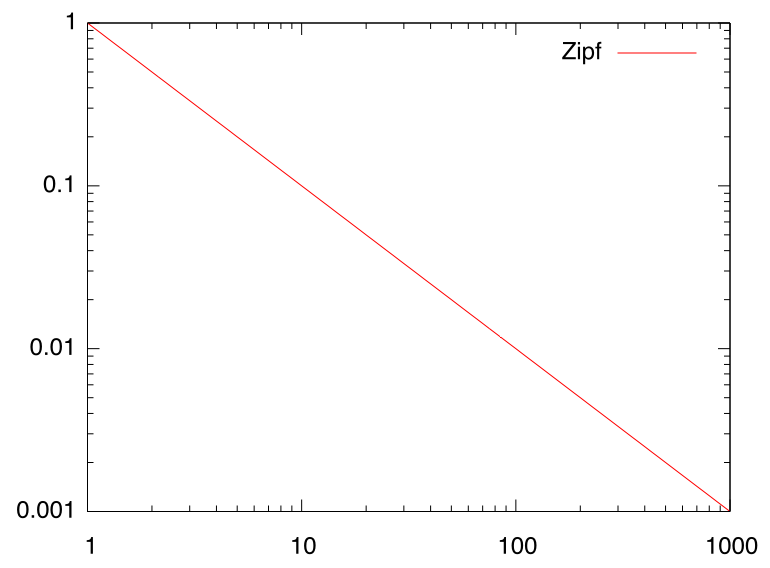
　一見フラクタル構造と関係無いところでも冪乗則が成立することがよくあります。たとえば、文章中でk番目に多く出現する単語の出現頻度は1/kに比例するというZipfの法則と呼ばれる経験則がありますが、 この関係は下図のように冪乗則に従います。

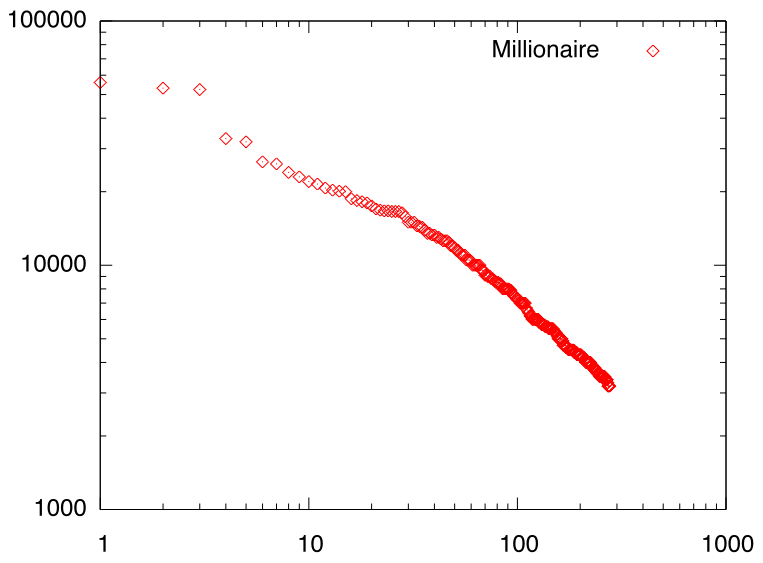
　また、富豪の収入ランキングも冪乗則に従うと言われています。世界の長者番付データをもとにしてグラフを書くと左図のようになり、確かに冪乗則が成立していることがわかります。またインターネットのトラフィックやSNSの様々なパラメタが冪乗則に従うことが知られており、このようないわゆる「スケールフリー構造(全体と一部が同じような形をしている構造をスケールフリー構造と呼びます)に関する研究が注目されています。冪乗則が観測される場合に必ず厳密なフラクタル構造が存在するとは限りませんが、何らかのフラクタル的な性質が存在するということは可能です。

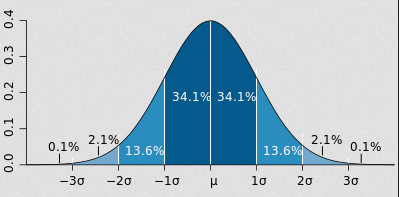
　世の中の多くのものは釣鐘状の正規分布に従うと思われている気がしますが、世の中のものは正規分布していると思う実際は正規分布をとる現象は世の中では小数派です。単語の出現頻度も富豪の収入ランキングも正規分布にならず、冪分布に従うわけですが、このような分布は実は全く珍しいものではなく、あらゆる場所で観測することができます。

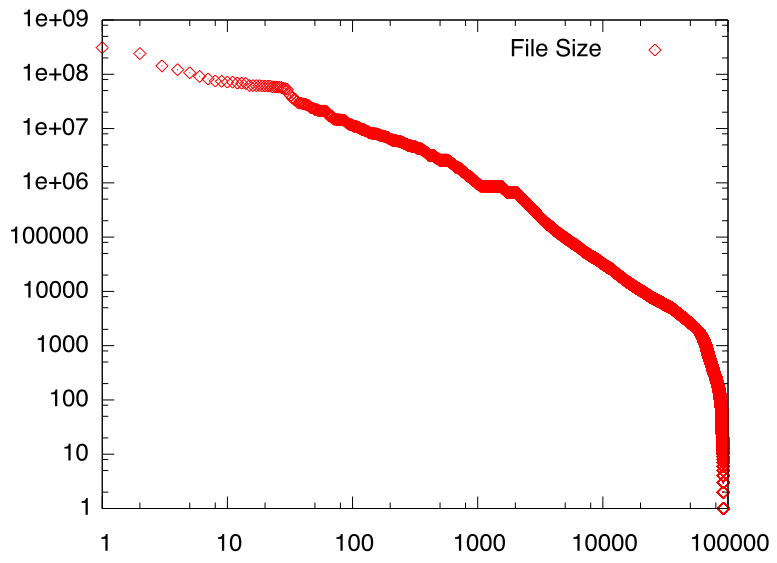
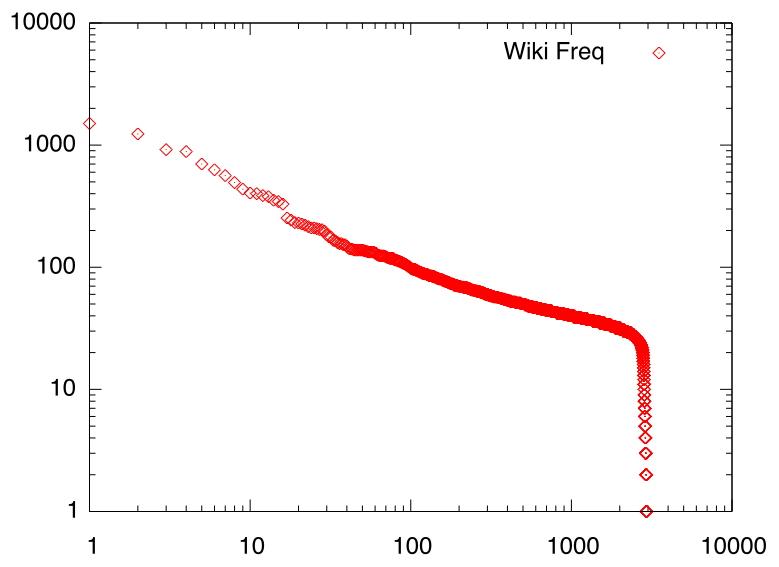
　下図は、私のホームディレクトリに入っているファイルを大きさの順に並べて両対数グラフ上にプロットしたものですが、単語の出現頻度と同じように、かなり奇麗な冪分布になっていることがわかります。またその下の図は、私がメモに使っているScrapboxプロジェクトのページアクセス回数を多い順に並べたものですが、やはり奇麗な冪分布になっています。

　このように、私の個人的なファイルについて調べてみると、ほぼすべてのデータが冪分布していることが判明してしまいました。私は大きなテキストファイルも小さなテキストファイルも持っていますし、大きな画像ファイルも小さな画像ファイルも持っています。私のコンピュータにはこれらの雑多なファイルがまとめて入っているという点がフラクタル的性質の元になっているのでしょう。

　メーリングリストの通信量、交通渋滞、ネットワークの通信量など、様々な複雑な事象において冪分布が報告されており、その発生する理由について様々な解析が行なわれていますが、どうやら、強い制約が存在しない場合、ほとんどあらゆる状況において複雑で大規模な事象は冪分布に従うと断言してしまって大丈夫な気がします。80:20の法則として有名なパレートの法則や、最近流行のロングテール現象もすべて冪分布にもとづく性質の表現であり、このような性質は極めてあたりまえのものなのかもしれません。ネットワークのような複雑なシステムにおいてはフラクタル的な冪分布が出現するのは当然であり、その現象が最近発見されて注目されたという点の方が不思議な気がします。

　複雑なシステムにおいて冪乗則が出現する理由を説明するための 様々なモデルが提案されています。しかし、あるモデルによって計算した結果が実際と一致していたとしても、全く異なる方法でも同じような結果が得られる可能性も高いので、本当にそのモデルが成立しているのかを証明することは難しそうです。一方、冪乗則の出現理由についてはわからなくても、冪乗則を効果的に利用する方法を工夫することは可能です。世の中のものはほとんどがフラクタル的であることを理解したうえで、それを考慮したシステムを設計して利用することを考えるとよさそうです。冪分布が生じる理由などについては数学者のTerence Tao氏の素晴らしい解説参考になるでしょう。